Lecture

R content

There is no separate R lab for today’s lecture. Instead, R code is (mostly) integrated into the slides. See below for an overview of all code presented in the slides.

R distribution functions

Function Template Purpose Binomial Normal
dxxx() Returns the density (height of PMF/PDF) dbinom(k, n, p) dnorm(x, mean, sd)
pxxx() Returns cumulative probability, P(X<=x) pbinom(k, n, p) pnorm(q, mean, sd)
qxxx() Returns the quantile (x-coordinate) from a given CDF probability qbinom(k, n, p) qnorm(p, mean, sd)
rxxx() Generate N random numbers from distribution rbinom(N, n, p) rnorm(N, mean, sd)

Note that all functions for the Normal distribution will assume standard normal if mean and standard deviation arguemnts are not provided. For example, R will interpret pnorm(5) as pnorm(5,0,1).

New ggplot functions

Function Purpose Example
geom_text() Add text to a plot geom_text( x=xcoordinate, y=ycoordinate, label = "text") (Note, these can all be aesthetics)
geom_vline() Add a vertical line to a plot geom_vline(xintercept=3)
geom_hline() Add a horizontal line to a plot geom_hline(yintercept=3)
geom_abline() Add a generic line of formula y=ax+b to a plot geom_abline(yintercept=3, slope = -2)
scale_x_continuous() Customize a continuous x-axis scale_x_continuous(name = "axis label", breaks=c(...), labels=c(...))
scale_y_continuous() Customize a continuous y-axis scale_y_continuous(name = "axis label", breaks=c(...), labels=c(...))

Examples

Reading and writing files with readr


library(readr)

### Read a csv (comma-separated values) ###
data <- read_csv("file.csv")

### Read a tsv (tab-separated values) ###
data <- read_tsv("file.tsv")

### Write a csv ###
example <- tibble(x = 1:10, y = 2:11)
write_csv(example, "file.csv")

### Write a tsv ###
example <- tibble(x = 1:10, y = 2:11)
write_tsv(example, "file.tsv")

Drawing random sample of rows with dplyr


## Sample 50 random rows from iris without replacement
iris %>% sample_n(50) -> iris50

## Sample 50 random rows from iris with replacement
iris %>% sample_n(50, replace=TRUE) -> iris50

## Sample 50%*nrow(iris) random rows from iris without replacement
iris %>% sample_frac(0.5) -> iris125

## Sample 50%*nrow(iris) random rows from iris with replacement
iris %>% sample_frac(0.5, replace=TRUE) -> iris125

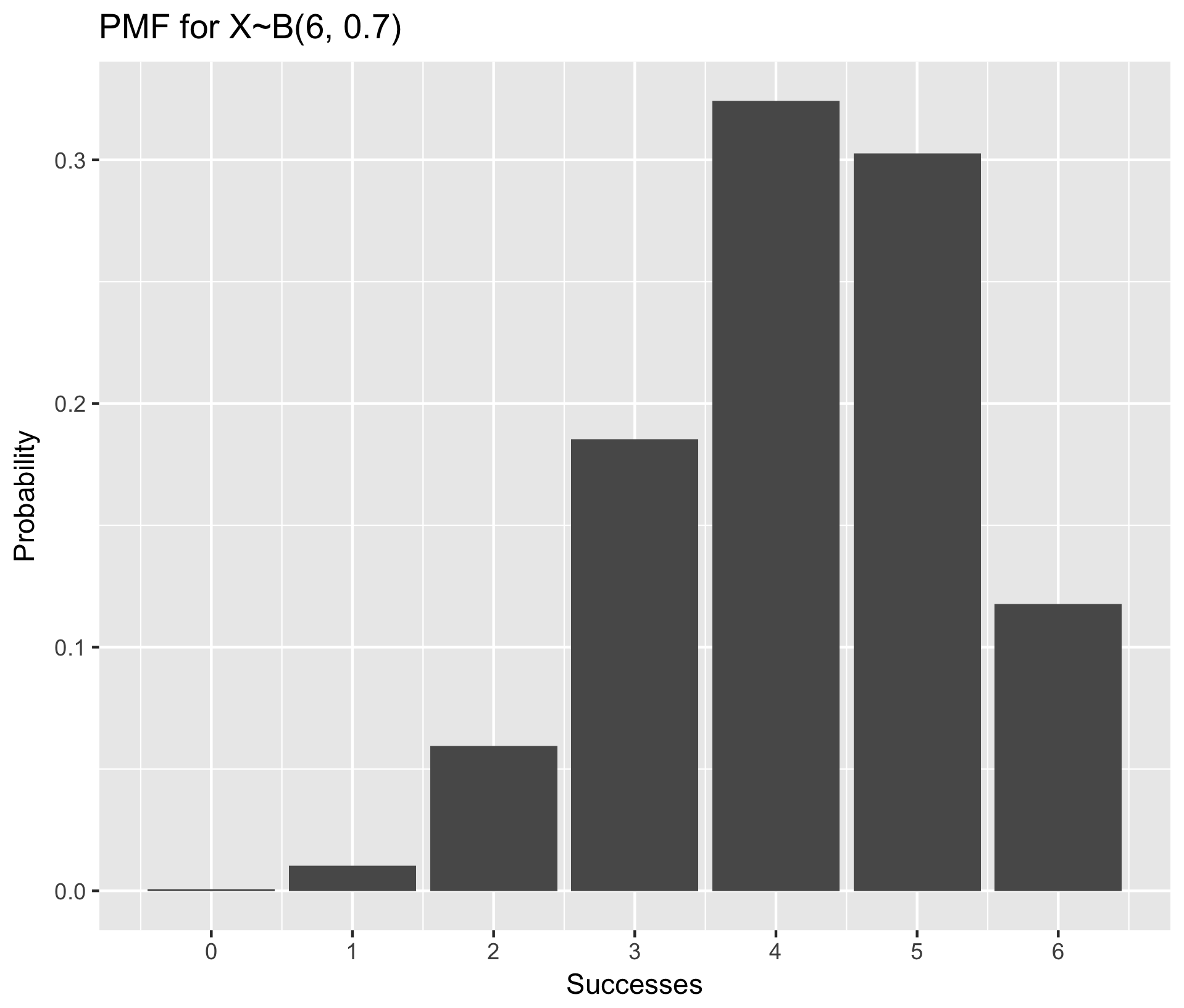
Visualize PMF using example X~B(6, 0.7) (ie, n=6, p=0.7)


library(purrr) ## Necessary for the map_dbl() function in step one

## Step One: Generate the data frame of probabilities for all k in 0:n
n <- 6
p <- 0.7
data.pmf <- tibble(k = 0:n, prob = map_dbl(0:n, dbinom, n, p))

## Step Two: make a bar plot with stat="identity" to make bar heights equal to their value in the data frame
ggplot(data.pmf, aes(x = k, y = prob)) + 
	geom_bar(stat = "identity") + 
	scale_x_continuous(name = "Successes", breaks=0:n) + 
	ylab("Probability") + 
	ggtitle("PMF for X~B(6, 0.7)")

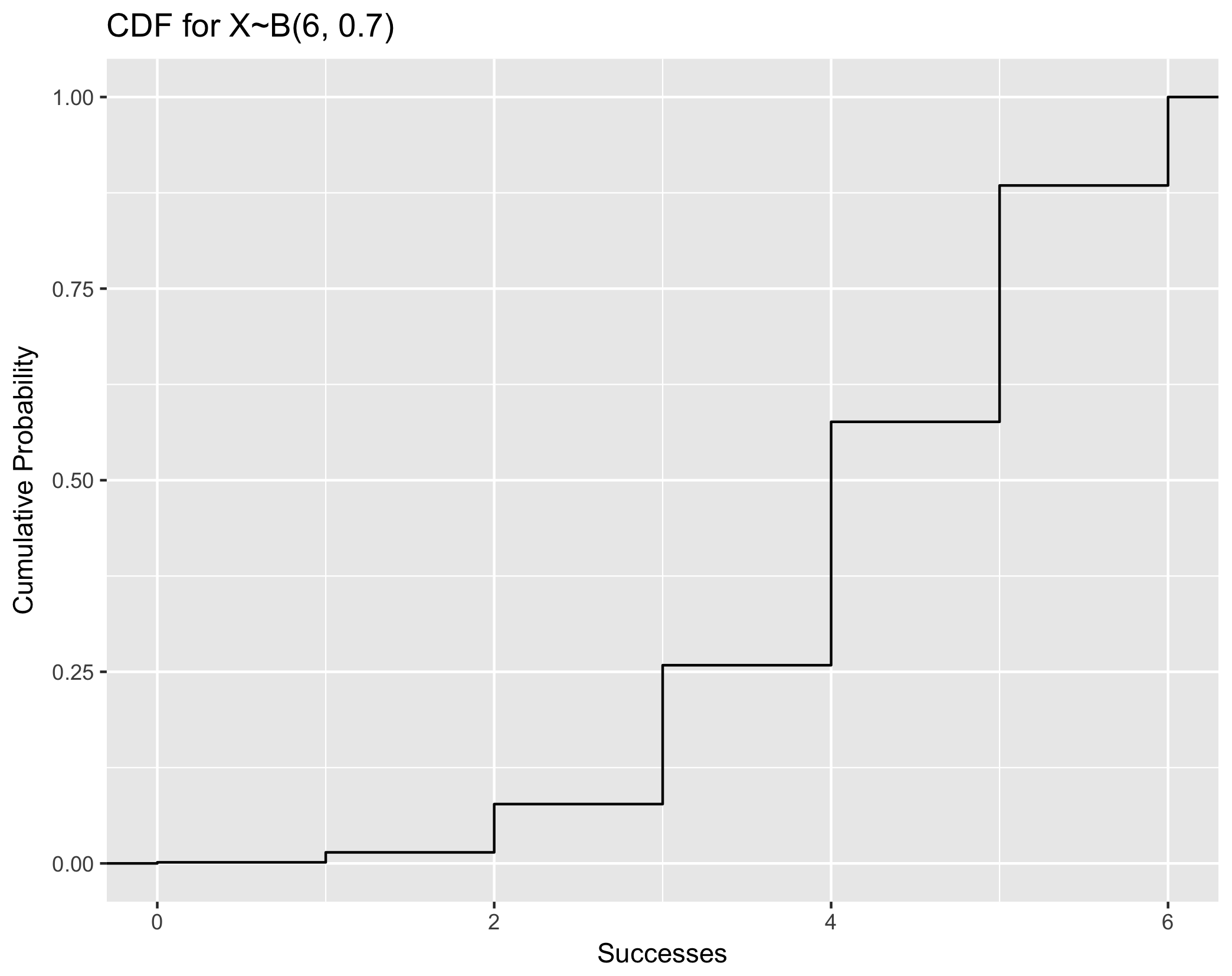
figure

Visualize CDF using example X~B(6, 0.7)


### Note that this plotting framework is generally applicable to both discrete and continuous CDF. ###

## Step One: Generate random numbers from the distribution of interest. Here, we generate 5000
data.cdf <- tibble(x = rbinom(5000, 6, 0.7))

## Step Two: plot with stat_ecdf()
ggplot(data.cdf, aes(x = x)) + 
	stat_ecdf() + 
	xlab("Successes") + 
	ylab("Cumulative Probability") + 
	ggtitle("CDF for X~B(6, 0.7)")

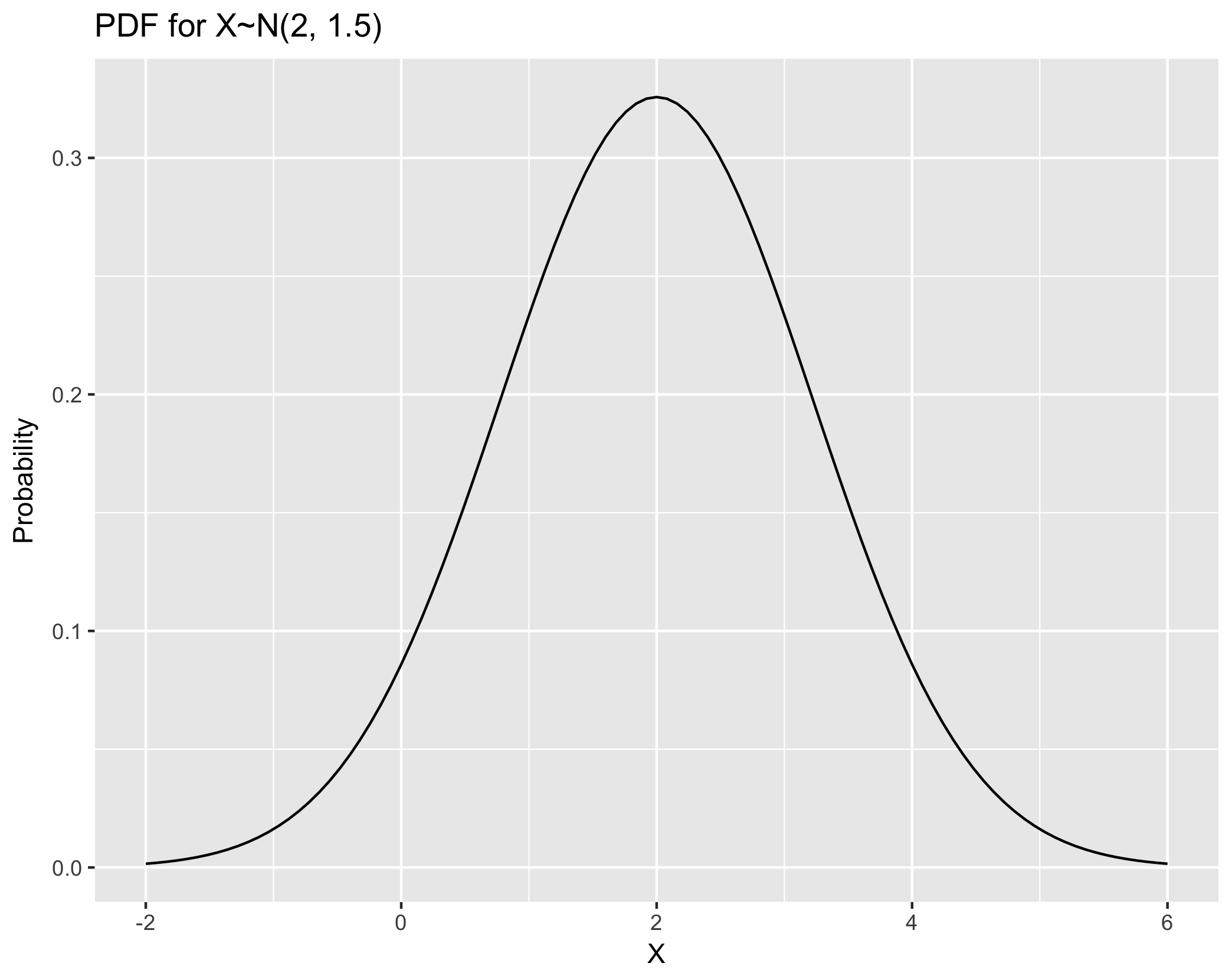
figure

Visualize PDF using example X~N(2, 1.5) (i.e. mean=2, variance=1.5)


## Step One: Create a data frame giving the x-axis range. +/- 3sd is usually ok
range.pdf <- tibble(x = c(2 - 4, 2 + 4))

## Step Two: plot with stat_function
ggplot(range.pdf, aes(x = x)) + 
	stat_function(fun = dnorm, args = list(mean = 2, sd=sqrt(1.5) )) + 
	xlab("X") + 
	ylab("Probability") + 
	ggtitle("PDF for X~N(2, 1.5)")

figure