Inclass exercises solutions, Day 9
Follow this link for day 9 materials and notes
ANOVA
Using the built-in dataset PlantGrowth, run an ANOVA to determine if plant weight differs across treatments.
Solution
> head(PlantGrowth)
weight group
1 4.17 ctrl
2 5.58 ctrl
3 5.18 ctrl
4 6.11 ctrl
5 4.50 ctrl
6 4.61 ctrl
> fit <- aov(weight ~ group, data = PlantGrowth)
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F)
group 2 3.766 1.8832 4.846 0.0159 *
Residuals 27 10.492 0.3886
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
### For demonstrative purposes, run a Tukey-Kramer test. Not necessary for every ANOVA!
> TukeyHSD(fit)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = weight ~ group, data = PlantGrowth)
$group
diff lwr upr p adj
trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711
trt2-ctrl 0.494 -0.1972161 1.1852161 0.1979960
trt2-trt1 0.865 0.1737839 1.5562161 0.0120064
Our null for the ANOVA is that all plant treatments have the same mean weight. Our alternative hypothesis is that at least one group has a different weight. ANOVA gives F = 4.806 with P=0.0159 which is significant at alpha = 0.05. We reject the null hypothesis and find evidence that at least one plant group has a different mean weight.
A post-doc Tukey test shows that trt1 and trt2 have significantly different weights (P=0.012) but that there is no evidence for weight differences for other group comparisons.
Pearson’s Correlation
Using the dataset wine.csv, run a correlation test to determine the strength and magnitude of the relationship between flavanoid and total phenol content across all wine cultivars.
Solution
> wine <- read.csv("wine.csv")
> head(wine)
Cultivar Alcohol MalicAcid Ash Magnesium TotalPhenol Flavanoids
1 1 14.23 1.71 2.43 127 2.80 3.06
2 1 13.20 1.78 2.14 100 2.65 2.76
3 1 13.16 2.36 2.67 101 2.80 3.24
4 1 14.37 1.95 2.50 113 3.85 3.49
5 1 13.24 2.59 2.87 118 2.80 2.69
6 1 14.20 1.76 2.45 112 3.27 3.39
NonflavPhenols Color
1 0.28 5.64
2 0.26 4.38
3 0.30 5.68
4 0.24 7.80
5 0.39 4.32
6 0.34 6.75
## Check linearity
> ggplot(wine,aes(x = Flavanoids, y = TotalPhenol))+geom_point()
## Run correlation
> cor.test(wine$Flavanoids, wine$TotalPhenol)
Pearson's product-moment correlation
data: wine$Flavanoids and wine$TotalPhenol
t = 22.824, df = 176, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8220088 0.8975164
sample estimates:
cor
0.8645635

The Pearson correlation between Flavanoids and TotalPhenol is R=0.86, and is significantly different from 0 (P<2.2e-16). Therefore these two quantities have strong and positive linear relationship.
Spearman’s Correlation
Using the ggplot2 dataset diamonds (you can access it like any built-in dataset if ggplot2 is loaded), run a non-parametric correlation test between diamond carat and price, specifically for diamonds with quality “Good”.
Solutions
> head(diamonds)
# A tibble: 6 x 10
carat cut color clarity depth table price x y z
1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
#### Subset for correlation
diamonds %>% filter(cut == "Good") -> good
## Check linearity
> ggplot(good,aes(x = price, y = carat))+geom_point()
## Run correlation
> cor.test(good$price, good$carat, method = "spearman")
Spearman's rank correlation rho
data: good$price and good$carat
S = 787830000, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.9599684 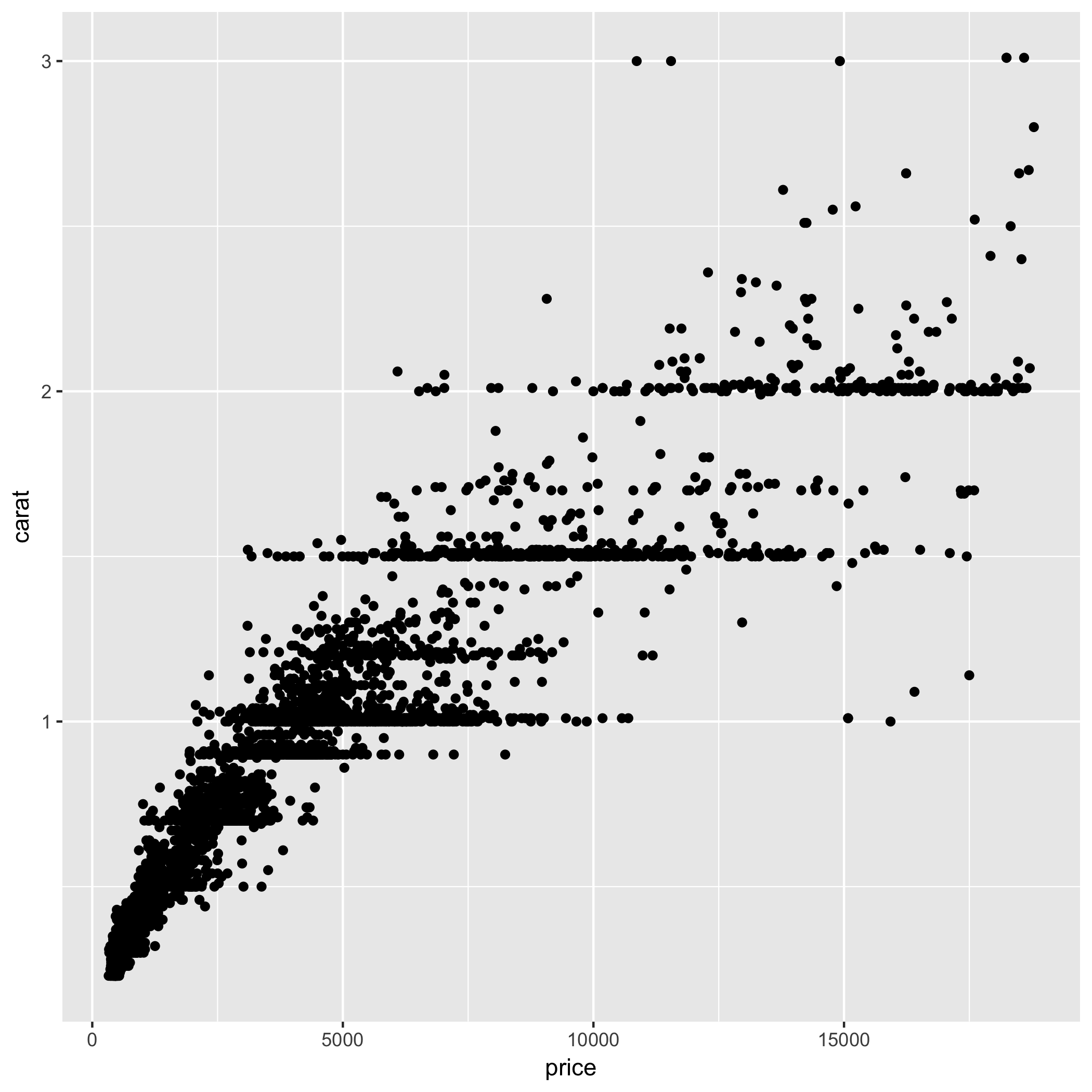
Diamond carat and price are not linearly related, as seen through plotting, so we must use a nonparametric correlation. The Spearman correlation between Flavanoids and TotalPhenol is R=0.96, and is significantly different from 0 (P<2.2e-16). Therefore these two quantities have strong and positive (but not linear!) relationship.
Regression
Using the dataset wine.csv, construct a linear model that can predict the amount of Flavanoids from the amount of non-flavanoid phenols (NonflavPhenols) across all wine cultivars. Then, predict the Flavanoid content for a wine with non-flavanoid phenols of 0.12.
## Check linearity with response on y axis
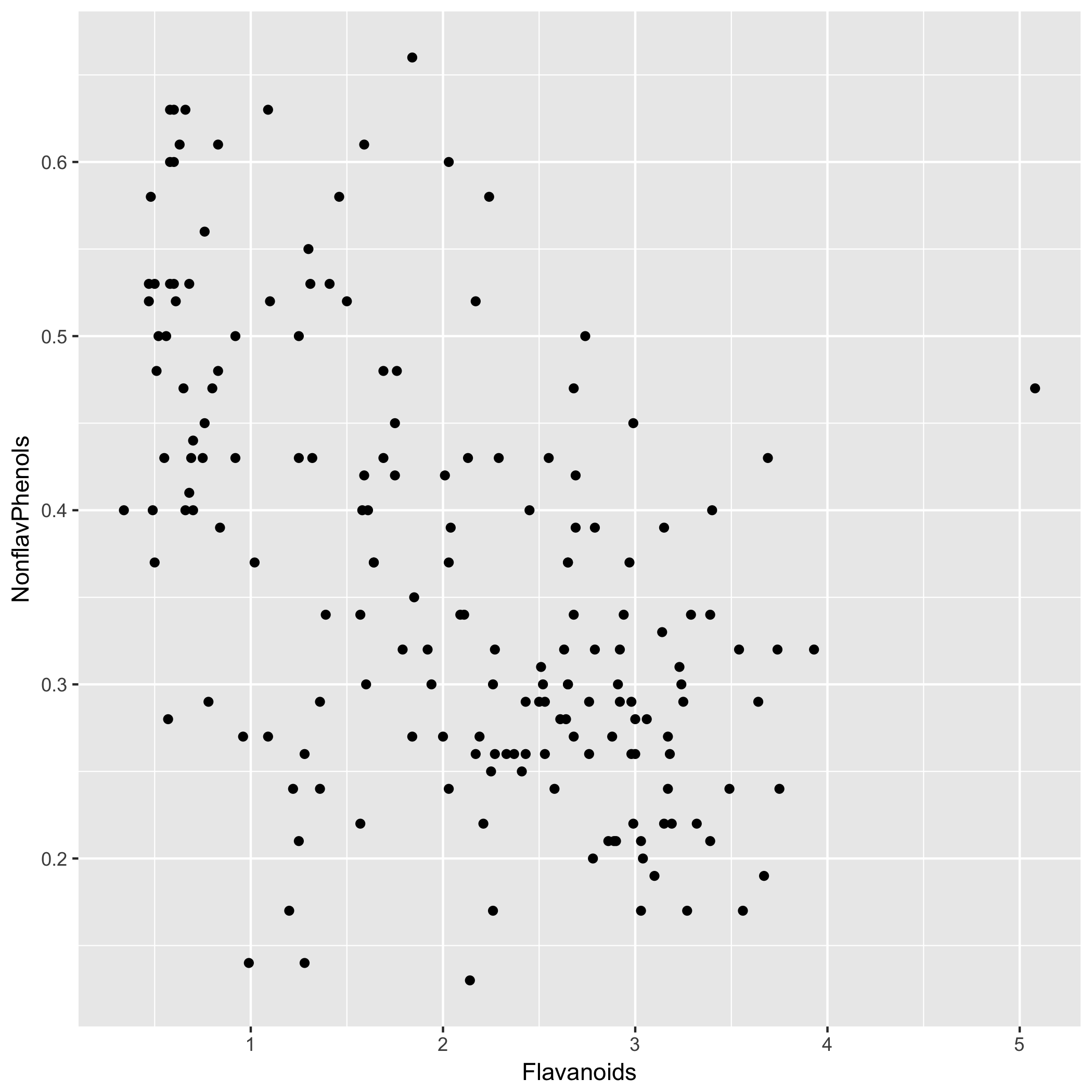
> ggplot(wine,aes(x = Flavanoids, y = NonflavPhenols))+geom_point()
## Fit model
> fit <- lm(NonflavPhenols ~ Flavanoids, data = wine)
> summary(fit)
Call:
lm(formula = NonflavPhenols ~ Flavanoids, data = wine)
Residuals:
Min 1Q Median 3Q Max
-0.29151 -0.06631 -0.01409 0.06859 0.31261
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.497855 0.017897 27.817 < 2e-16 ***
Flavanoids -0.067020 0.007917 -8.465 9.74e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1052 on 176 degrees of freedom
Multiple R-squared: 0.2893, Adjusted R-squared: 0.2853
F-statistic: 71.66 on 1 and 176 DF, p-value: 9.739e-150.9599684
### Note the broom package!
> tidy(fit)
term estimate std.error statistic p.value
1 (Intercept) 0.49785537 0.017897438 27.81713 2.490523e-66
2 Flavanoids -0.06701989 0.007917322 -8.46497 9.739231e-15
> glance(fit)
r.squared adj.r.squared sigma statistic p.value df logLik
1 0.289336 0.2852981 0.1052129 71.65571 9.739231e-15 2 149.2495
AIC BIC deviance df.residual
1 -292.4991 -282.9537 1.948277 176
Check linearity:
Add regression line:
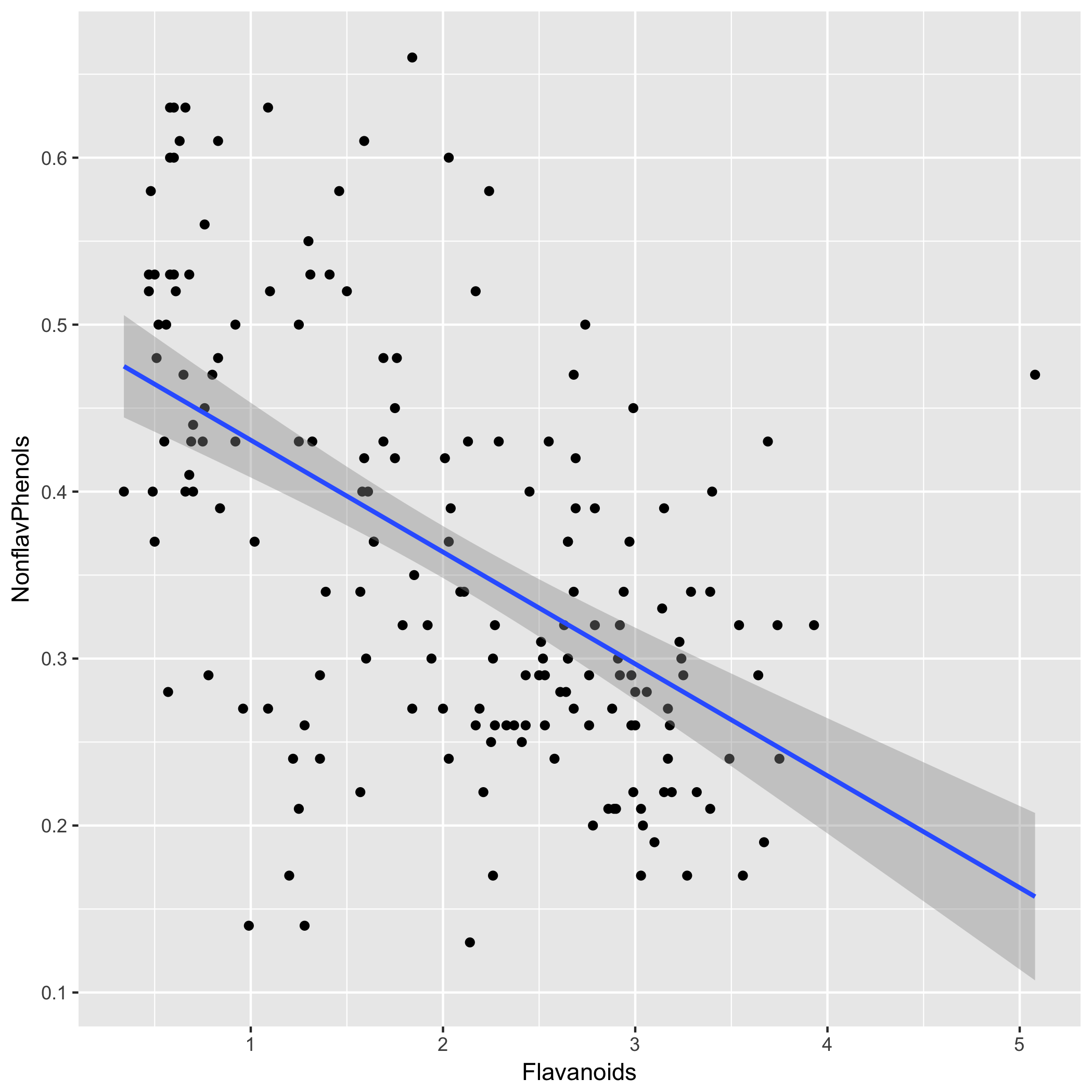
Our model shows a moderate but significant relationship between flavanoids and non-flavanoid phenols. Our model’s (P=9.74e-15) is highly significant and indicates that flavanoid content can explain ~29% of variation in non-flavanoid phenols. Therefore, the model does not explain the majority of variation in non-flavanoid phenols.
The flavanoid coefficient is -0.067 (P=9.74e-15), meaning that for every unit increase in flavanoid content, we expect non-flavanoid phenols to decrease by 0.067 units on average. The intercept is 0.498 (P=2.49e-66), so wine with 0 flavanoid content is expected to contain 0.497 units of non-flavanoid phenols, although this quantity is probably not meaningful in the context of actual wine.